• 微积分总览
  • differential calculus 微分学
  • integral calculus 积分学 integral(from whole)
  • 函数1 和 函数2 的关系
• 导数总览
  • 几个重要的函数导数
• 极值和二阶导数
  • 一阶导数 求 极值点 ，导数=0
  • 二阶导数 确定 极值点性质
  • 距离／速度 / 加速度 的例子
  • Convex ,bending up, 凸 , 极小值 , ex: x²
  • Concave, bending down ,凹, 极大值
  • 二阶导数性质
  • 导数应用例子
• 指数函数 y=eˣ
  • 重要性质:
  • eˣ 构建:
  • 银行存款和e的联系
  • y' = dy/dx = ay 的情况, y = eªˣ
• 积分总览
• sin / cos 的导数
  • sin/cos 勾股定理
  • 弧度 等于半径为1圆周上对应的弧长 ( 圆周长2π )
  • 弧度θ 对应的扇形面积，等于 θ/2
  • sinθ < θ ( θ>0 , 弧度制)
  • tanθ > θ ( 0< θ <π/2 , 弧度制 )
  • dsinx/dx = cosx 的证明
    • sin(ɑ+β)=sinɑ·cosβ + cosɑ·sinβ
    • cos(ɑ+β)=cosɑ·cosβ - sinɑ·sinβ
• 乘法法则 Product Rule
• 除法法则 Quotient Rule
• the Chain Rule for f(g(x))
• Limits
  • 洛必塔法则: 0/0型不定式极限
• Continuous Function
  • 函数不连续的例子:
• Inverse function 逆函数
• derivatives of lny and sin⁻¹(y) (f⁻¹型导数)
• Growth Rate and Log Graphs
• 线性近似 Linear Approximation
• Newton's Method 牛顿法
• 泰勒级数 Taylor series
• 幂级数 Power Series
  • eˣ 的幂级数
  • sin, cos的级数
  • 欧拉公式 Euler's Great Formular
  • 几何级数 geometric series

微积分总览

differential calculus 微分学

从距离函数 f->速度函数s

integral calculus 积分学 integral(from whole)

从 速度函数s->距离函数f

函数1 和 函数2 的关系

• 函数f 在某个t的函数值，描述的，是函数s的图像面积
• 函数s 在某个t的函数值， 是 函数f 在t 时刻的斜率
• f= ∫s(t) (f1是f2的积分)
• df/dt = s (f2是f1的导数)

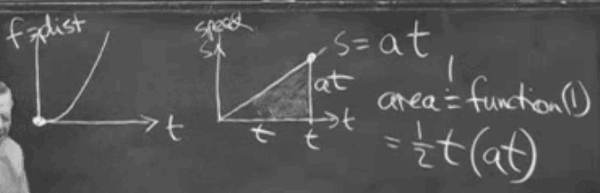
导数总览

几个重要的函数导数

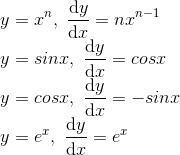
sinx

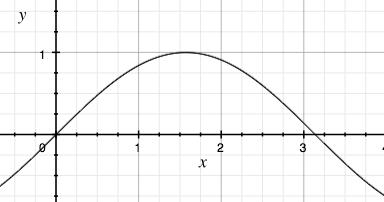
eˣ

极值和二阶导数

一阶导数 求 极值点 ，导数=0

二阶导数 确定 极值点性质

距离／速度 / 加速度 的例子

距离函数f 的一阶导数 dy/dx 是 速度函数, 是f图像的斜率slope

二阶导数是 d²y/dx² 加速度函数, 是f图像的弯曲度 bending

Convex ,bending up, 凸 , 极小值 , ex: x²

Concave, bending down ,凹, 极大值

二阶导数性质

极值点，二阶导数为负值，局部最大值（极大值）

极值点，二阶导数为正值，局部最小值（极小值）

inflection point 拐点: 二阶导数为0的点，也是二阶导数开始改变符号的地方

导数应用例子

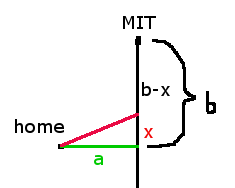
开车到MIT， 从家开车到麻省高速的车速是30,的垂直距离是a, 麻省高速的车速为60， 求最省时间的开车路线（红色)

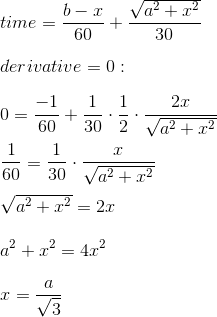
注意点:

1. 如果MIT距离不够远，即MIT 位于x段，需要特殊处理一下
2. 理论上，需要再求一下2阶导数，来确定是极小值，但是这里f''的符号，可以通过f'的单调性来求出，简单说：x>0时f'(x)>0,斜率变化为正，f''>0 (why?)

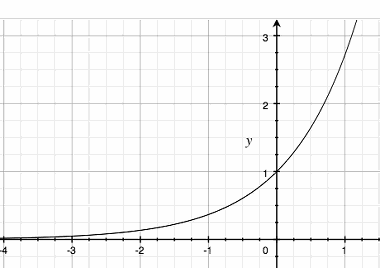
指数函数 y=eˣ

重要性质:

1. 导数是其自身: dy/dx = y
2. eˣ·eʸ= eˣ⁺ʸ , 推论: eˣ·e⁻ˣ =1 , e⁻ˣ=1/eˣ, 互为倒数

eˣ 构建:

从x=0, eˣ=1 开始, 根据性质: (eˣ)'=eˣ , 无限展开

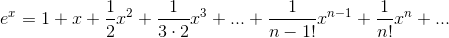
当x=1时，指数级数的值就是e，近似2.7

1+x <= eˣ

银行存款和e的联系

假设年利率是 100%,

按年结算，第2年的总存款变为 (1+1)¹=2

按月结算，第12个月的总存款变为 (1+1/12)¹²= 2.613035290224676

按天结算，第365天的总存款变为 (1+1/365)³⁶⁵ = 2.7145674820219727

按N 结算，(1+1/N)ᴺ -> e

y' = dy/dx = ay 的情况, y = eªˣ

积分总览

1. 函数2是函数1的导数
2. 函数1是函数2的积分
3. 积分=函数1=函数2图像下的面积

sin / cos 的导数

sin/cos 勾股定理

(cosθ)²+(sinθ)²=1

弧度 等于半径为1圆周上对应的弧长 ( 圆周长2π )

弧度θ 对应的扇形面积，等于 θ/2

S = πr²/(2π) * θ = θ/2

sinθ < θ ( θ>0 , 弧度制)

作图证明:

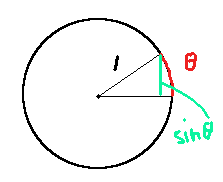
tanθ > θ ( 0< θ <π/2 , 弧度制 )

作图证明:

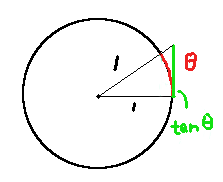
1. tanθ = sinθ/cosθ, 如果直角三角形的邻边=1, 则对边就=tanθ
2. 三角形面积 tanθ/2 > 扇形面积 θ/2 => tanθ > θ

由此可以推出, sinθ/θ > cosθ ,

所以， 当 θ->0 时，sinθ/θ = 1

dsinx/dx = cosx 的证明

sin(ɑ+β)=sinɑ·cosβ + cosɑ·sinβ

cos(ɑ+β)=cosɑ·cosβ - sinɑ·sinβ

证明:

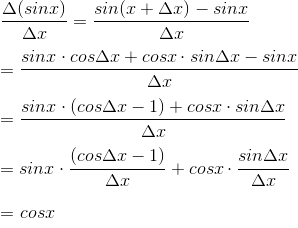
第一项后半部分的比值，其实就是0点处cosx 的斜率=0

乘法法则 Product Rule

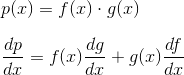
图解:

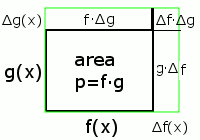
如图所示:

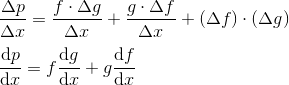
eg:

x³ = x²·x

d/dx(x³) = x²·1 + x·2x = 3x²

d/dx(f(x)³)= 3f(x)²·df/dx

除法法则 Quotient Rule

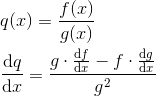
下乘上导，减上乘下导，除以 下下

利用乘法法则推演:

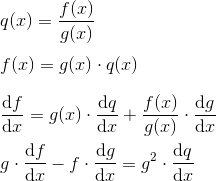
the Chain Rule for f(g(x))

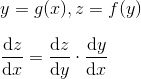
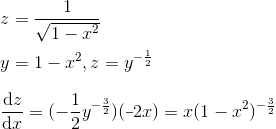
Limits

(an)ᵇⁿ dangerous case:

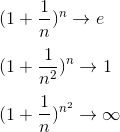
洛必塔法则: 0/0型不定式极限

使用导数求解 0/0 型

 1. 当x趋于a时，函数f(x)及g(x)都趋于零
 2. 在点a的某去心邻域内，f'(x)及g'(x)都存在且g'(x)不为零
 3. 若f'(x)/g'(x)极限存在，则有 f(x)/g(x)的极限 等于 f'(x)/F'(x)的极限 (lim x->a) 。

if f(x)→0, as x→0 ; g(x)→0, as x→0 ;

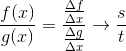
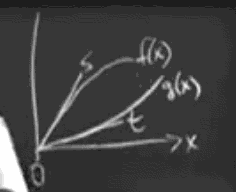
极限不存在的例子:

√x 在 x→0时极限不存在。

函数连续是较弱的性质，较强的性质的可导：可导必然连续，连续不一定可导。

Continuous Function

Continuous f(x) at x→a,
means f(x)→f(a) as x→a.

also means , for any ϵ choosen by Socrates, Plato can find a δ so that:
if |x-a|<δ then |f(x)-f(a)|<ϵ 

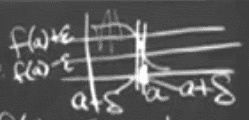
函数不连续的例子:

x→0 时函数不连续:

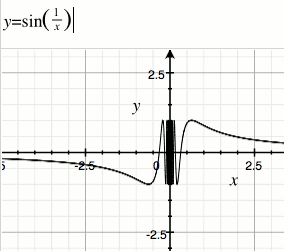
修改一下，使其在 x→0 时连续:

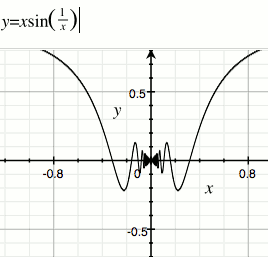
Inverse function 逆函数

y=f(x) , x=f⁻¹(y)

指数函数eˣ的逆函数是 lny

y=eˣ , x= lny
ln(y·Y) = lny + lnY   (1)
ln(yⁿ) = n·lny  (2)

证明(1):

y=eˣ 
Y=e^X 
y·Y = eˣ·e^X = e^(x+X)
ln(y·Y) = x+X = lny + lnY

证明(2):

ln(y²)=ln(yy)=lny+lny=x+x =2x = 2lny
可以推出:
ln(yⁿ)=nlny

所有 逆函数图像和原函数图像，沿y=x 的直线对称

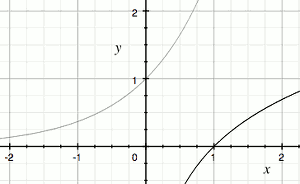
对数函数，即指数函数的逆函数的导数:

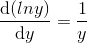
derivatives of lny and sin⁻¹(y) (f⁻¹型导数)

f⁻¹(f(x))=x   (1)
f(f⁻¹(y))=y   (2)

上面的式子告诉我们，如果知道怎么求 f(x)的倒数，用链式法则就可以求出f⁻¹(y)的倒数。

lny example 1:

ln(eˣ)=x (对数函数的定义)
令y=eˣ , 两边求导:
d(lny)/dy · d(eˣ)/dx = 1
d(lny)/dy · eˣ = 1
d(lny)/dy · y = 1
由此得出:
d(lny)/dy = 1/y

在我们求导 xⁿ的时候，如果n=0 , 则 (xⁿ)'＝0, 我们并不能获得 x的⁻¹次幂，事实上，不存在幂函数的导数能得到⁻¹次幂。

这就像一个遗漏，现在 lny 填补了这个遗漏。

lny example 2:

eˡⁿʸ=y
(eˡⁿʸ) · d(lny)/dy = 1
d(lny)/dy = 1/y

x = sin⁻¹y (arcsin)

y = sin( sin⁻¹y )
两边求导:
1 = cos( sin⁻¹y ) · d(sin⁻¹y)/dy 
因为 sin²x + sin²y =1, 得出
1 = √(1-y²)· d(sin⁻¹y)/dy 
d(sin⁻¹y)/dy = 1 /( √(1-y²) )

同理可得:
d(cos⁻¹y)/dy = -1 /( √(1-y²) )

我们发现：

d(sin⁻¹y)/dy + d(cos⁻¹y)/dy =0

常数项的导数为0，由此可知, arcsin + arccos 的和是一个常数，事实上，arcsin + arccos = 直角三角形的两个锐角的和 = π/2

Growth Rate and Log Graphs

TODO

线性近似 Linear Approximation

x 在 a点的导数，近似等于:

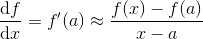
由此得出:

• f(x) ≈ f(a)+(x-a)·f'(a) (1)
• x-a ≈ - F(a)/F'(a) (2，用于解F(x)=0方程)

example 1: 求√9.06

f(x) = √x = x⁰ᐧ⁵
f'(x) = 1/2 · x⁻⁰ᐧ⁵
choose a=9
f(a)=3
f'(a) = 1/6
√9.06 ≈ 3 + (9.06-9)*1/6 = 3.01

example 2: 解方程: F(x) = x²-9.06 =0

choose a=3
F(a)= 9-9.06 = -0.06
F'(a) = 2a = 6
x-3 = -(-0.06/6)
x = 3.01

example 3: 求 e⁰ᐧ⁰¹

f(x) = eˣ
choose a=0
f(0) =1
f'(0) =1
e⁰ᐧ⁰¹≈ f(a)+(0.01-a)f'(a) = 1+0.01

我们可以看到 eˣ = 1+x

1+x 其实就是 eˣ 幂级数 从常数项和线性项之后的拦腰截断。 当 x 很小的时候，x < 0.1 , eˣ 近似等于 1+x>

Newton's Method 牛顿法

使用线性近似求的近似值 x₁后, 利用 x₁和公式2进行下一轮迭代，以获得更小的误差。

解方程: F(x) = x²-9.06 =0

a=3.01 
F(a) = 0.0001
F'(a) = 2a = 6.02
x-a ≈ -(F(a)/F'(a))
x ≈ 3.01 - ( 0.0001/6.02  )       // (x*x = 9.0600000002759)

泰勒级数 Taylor series

在数学中，泰勒级数 用无限项连加式级数来表示一个函数，这些相加的项由函数在某一点的导数求得。

定义：如果 在点x=x0具有任意阶导数，则幂级数

称为 在点x0处的泰勒级数

特别的，取x0=0，得到的级数

称为麦克劳林级数。函数 的麦克劳林级数是x的幂级数

幂级数 Power Series

用函数f(x) 在x=0处的各级导数，来描述函数f(x)

f(x) = a + a₁x + a₂x² + a₃x³ + ...

eˣ 的幂级数

因此 e⁰=1, (eˣ)'=eˣ , e^n的阶导数等于1

所以:

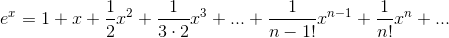
sin, cos的级数

sinx 各级导数如下：

所以,sinx 的幂级数构建如下:

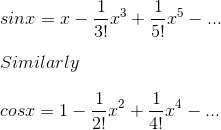
我们看到，cosx的幂级数，都是偶次幂，所以 cos(-x)=cos(x), 这给了我们另一个观察奇/偶函数的视点。

欧拉公式 Euler's Great Formular

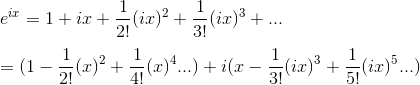
我们看到:

eⁱˣ= cosx + i·sinx

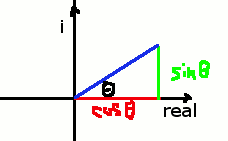
把 x 改成θ , eⁱᶿ= cosθ + i·sinθ

函数图像:

几何级数 geometric series

1 + x + x² + x³ + ...

当 |x| < 1 时,

1/(1-x) = 1 + x + x² + x³ + ...

对等式求积分:

-ln(1-x) = x + x²/2 + x³/3 + ...

for r != 1 :

1 + r + r²+ ... + rᵏ = (rᵏ⁺¹-1)/(r-1) (算法课程中提及)