在 Java 中实现一个二叉查找树

原文：https://www.studytonight.com/java-examples/implementing-a-binary-search-tree-in-java

二叉查找树是由节点和链接组成的非线性数据结构。这是一种二叉树，这意味着每个节点最多可以有两个子节点。

一个二叉查找树还必须遵循给定的两个条件。

1. 左节点的值应该小于其父节点的值。
2. 右节点的值应该大于其父节点的值。

对于树的所有节点，上述两个条件必须为真。下图显示了一个二叉查找树。

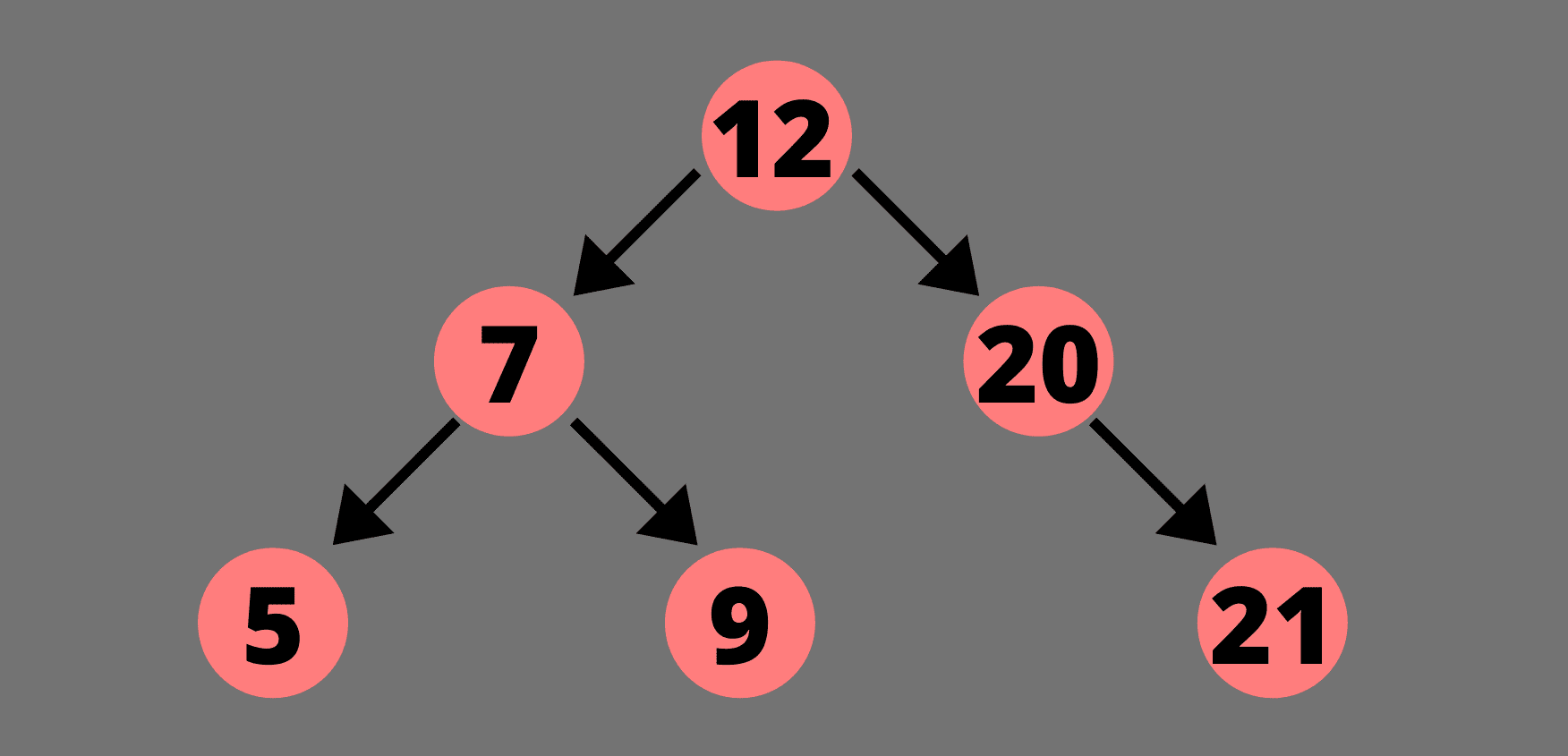
二叉树节点的一般结构如下所示。它由一个值和两个指针组成——一个指向它的左子，另一个指向它的右子。

二叉查找树的节点类别如下所示。

class BSTNode
{
    int value;
    BSTNode leftChild;
    BSTNode rightChild;

    BSTNode(int val)
    {
        this.value = val;
        this.leftChild = null;
        this.rightChild = null;
    }
}

一个二叉查找树可以有四个基本操作- 插入、删除、搜索和遍历。让我们学习如何在 Java 中实现二叉查找树。

插入二叉查找树

在二叉查找树中插入一个元素非常简单。我们只需要用下面的算法找到它的正确位置。这样做是为了确保插入后的树符合二叉查找树的两个必要条件。

• 如果新值小于当前节点值，则递归到左子。
• 如果新值大于当前节点值，则递归到其右子节点。
• 如果当前节点为空，则在此位置添加新值。

public static BSTNode insert(int value, BSTNode current)
{        
    if(current == null)
    {
        BSTNode newNode = new BSTNode(value);
        return newNode;
    }
    else
    {
        if(value < current.value)
            current.leftChild = insert(value, current.leftChild);
        else
            current.rightChild = insert(value, current.rightChild);
    }        
    return current;
}

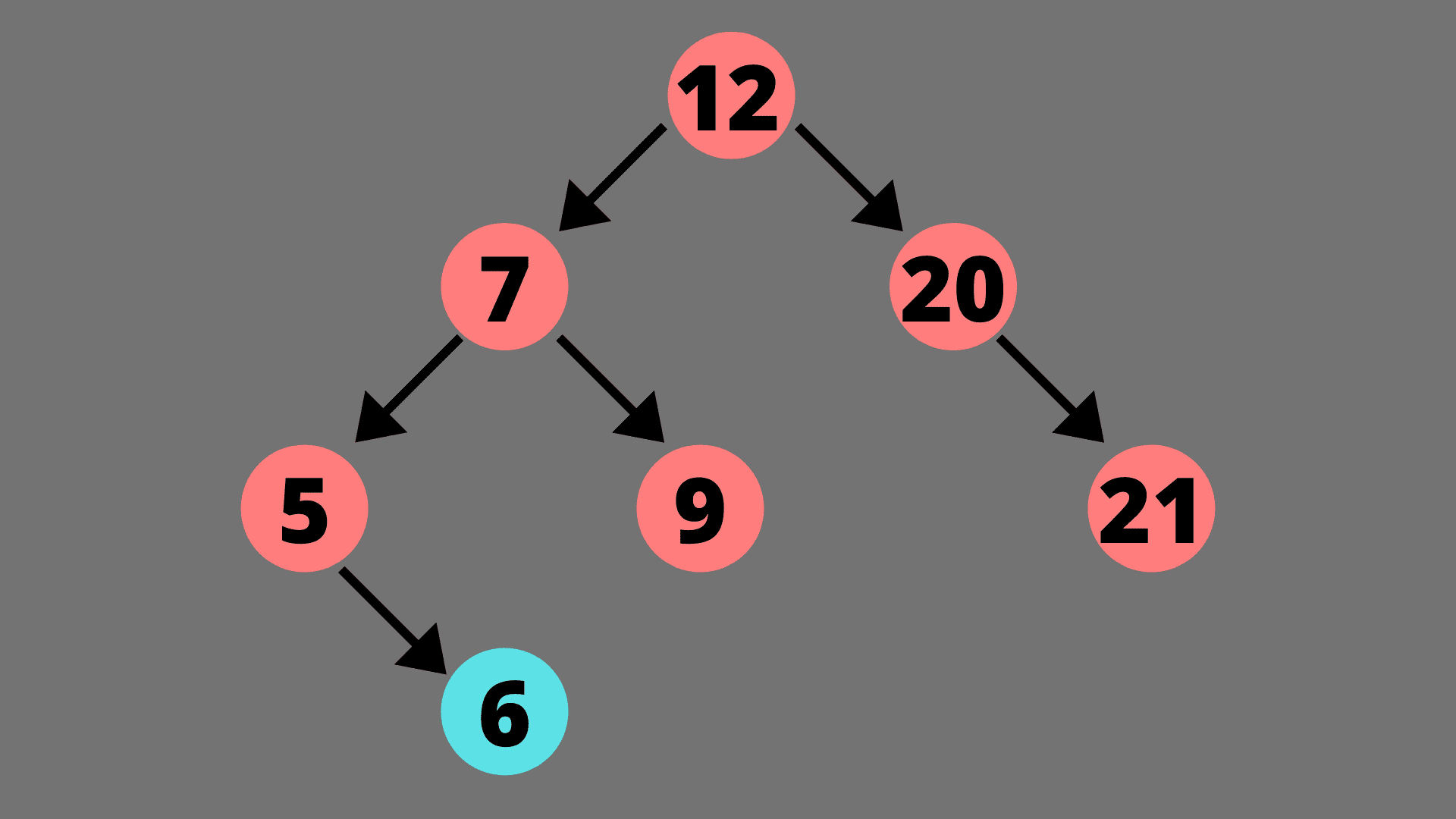
例如让我们尝试将值 6 插入到下面的树中。

我们首先将 6 与根值 12 进行比较。6 比 12 小，所以我们将移动到左子树，并将 6 与左子树的根进行比较。6 比 7 小，所以我们将再次移动到左边的子树。现在，6 大于 5，所以我们移到右边的子树。但是右边的子树为空或者不存在，所以会在这个位置添加新节点。

在二叉查找树搜索

在二叉查找树中搜索一个值遵循与我们讨论的元素插入基本相同的逻辑。唯一的区别是，如果在任何时刻当前节点为空，则表明该值不在树中。我们将返回 False，而不是插入值。

• 如果当前节点的值与我们试图找到的值匹配，则返回真。
• 如果当前节点的值大于我们试图找到的值，则递归到左边的子节点。
• 如果当前节点的值小于我们试图找到的值，则递归到右边的子节点。
• 如果当前节点为空，则返回假。

该方法的代码如下所示。

public static boolean search(int key, BSTNode current)
{
    if(current == null)
        return false;
    if(current.value == key)
        return true;
    else
    {
        if(key < current.value)
            return search(key, current.leftChild);
        else
            return search(key, current.rightChild);
    }                    
}

在二叉查找树删除

从二叉查找树中删除节点的过程比插入和搜索要复杂一些。首先，我们需要找到要删除的节点。这部分的逻辑将与插入和搜索中讨论的相同。

在找到正确的节点后，我们需要根据节点的性质遵循以下步骤之一。

• 如果它是一个叶节点(一个没有子节点的节点)，那么我们可以简单地用空替换那个节点。
• 如果节点只有一个子节点，那么它将被删除，子节点将占据其位置。
• 如果节点有两个子节点，那么它将被删除，并且来自其左子树的最大节点取其位置，或者来自其右子树的最小值取其位置。对于我们的代码，我们将使用右子树中的最小值。

public static BSTNode delete(int value, BSTNode current)
{
    if(current == null)
        return current;        
    if(value < current.value)
        current.leftChild = delete(value, current.leftChild);
    else if(value > current.value)
        current.rightChild = delete(value, current.rightChild);
    else if(value == current.value)
    {
        if(current.leftChild != null && current.rightChild != null)
        {
            int min = current.rightChild.value;
            BSTNode temp = current.rightChild;
            while(temp.leftChild != null)
            {
                min = temp.leftChild.value;
                temp = temp.leftChild;
            }
            current.value = min;
            current.rightChild = delete(min, current.rightChild);
        }            
        else if(current.leftChild == null)
            return current.rightChild;
        else if(current.rightChild == null)
            return current.leftChild;            
        else
            return null;
    }
    return current;
}

例如，让我们试着从下面的树中删除 12、20 和 9。

从二叉查找树删除 12 个

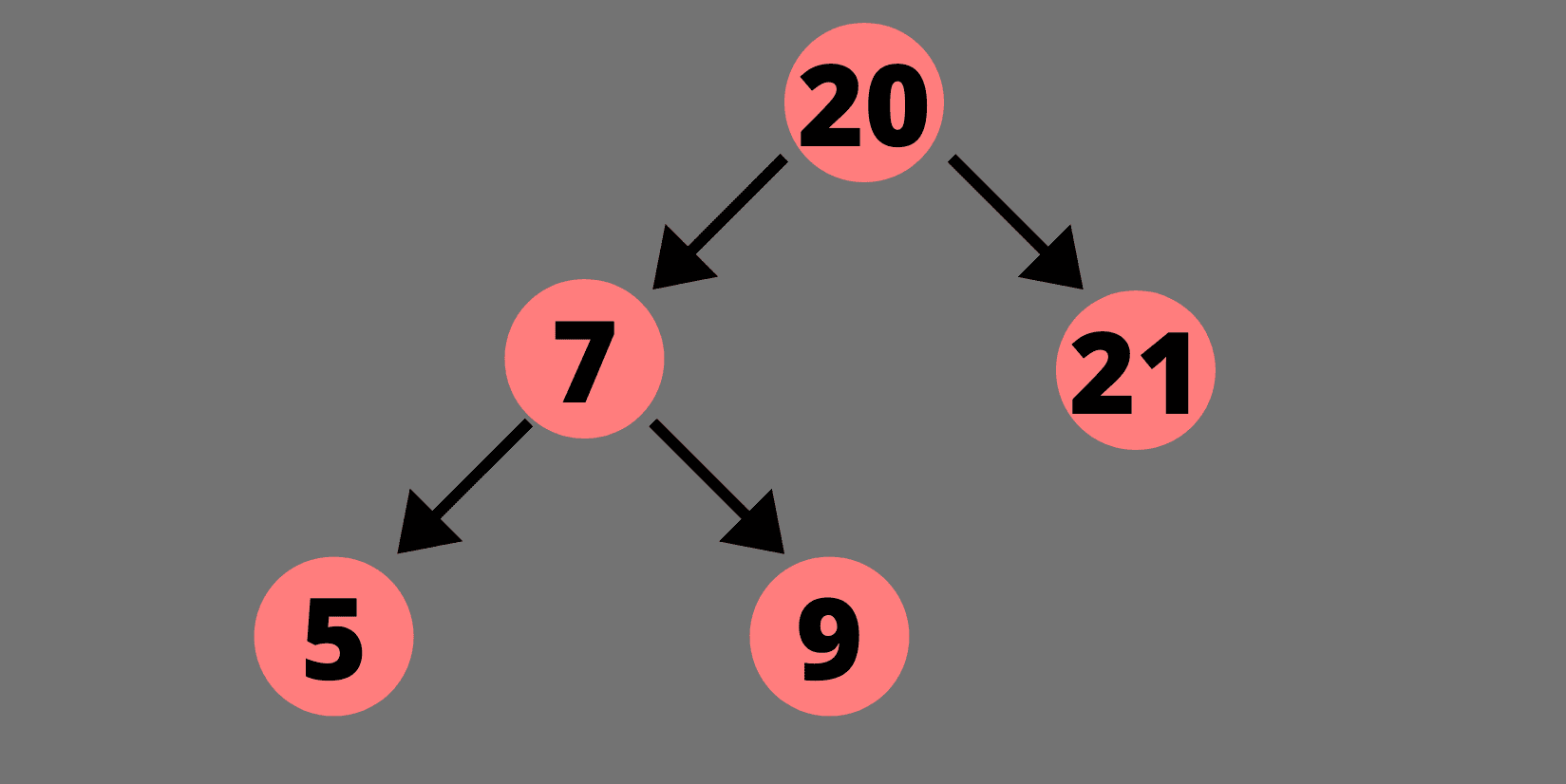
从二叉查找树删除 20 个:

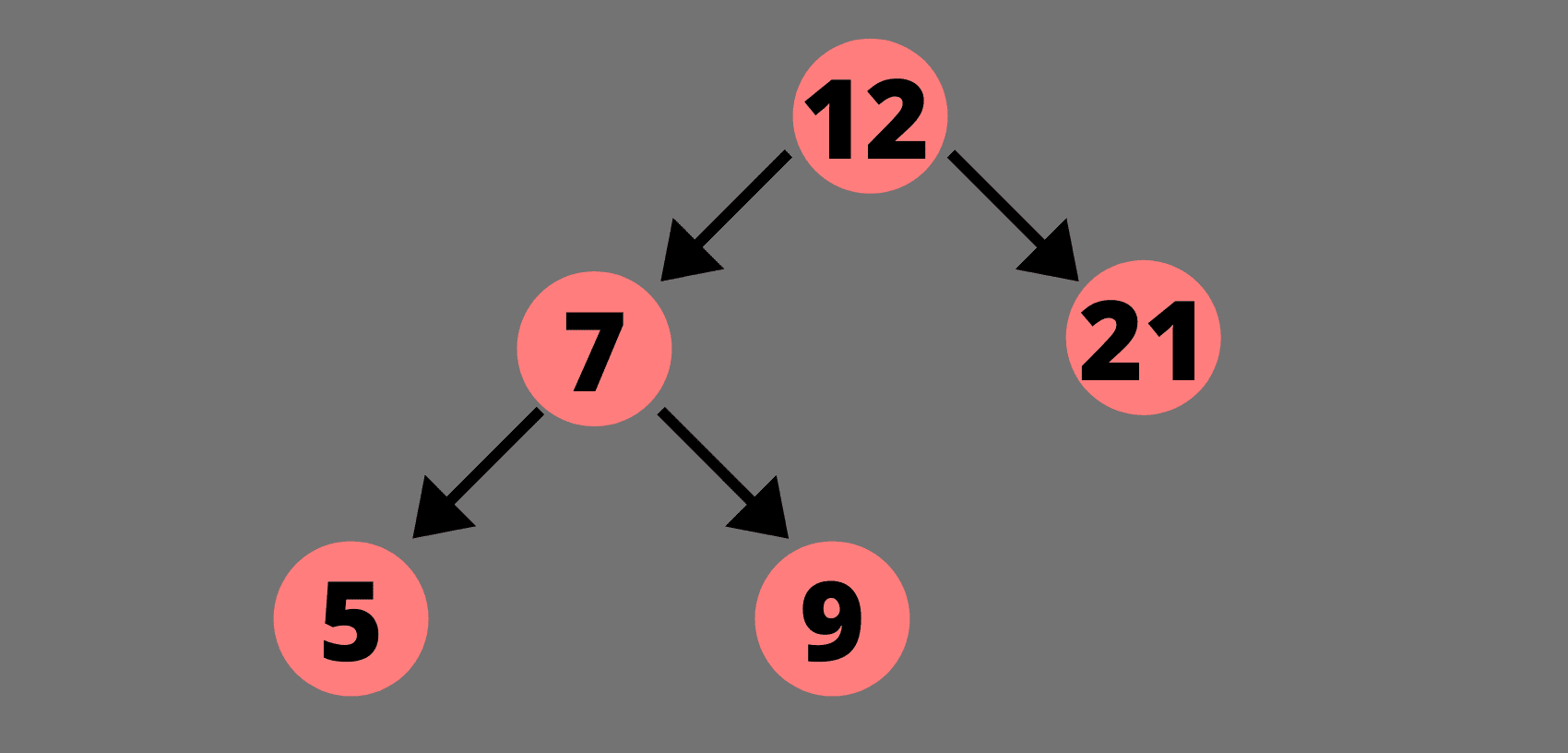
从二叉查找树删除 9:

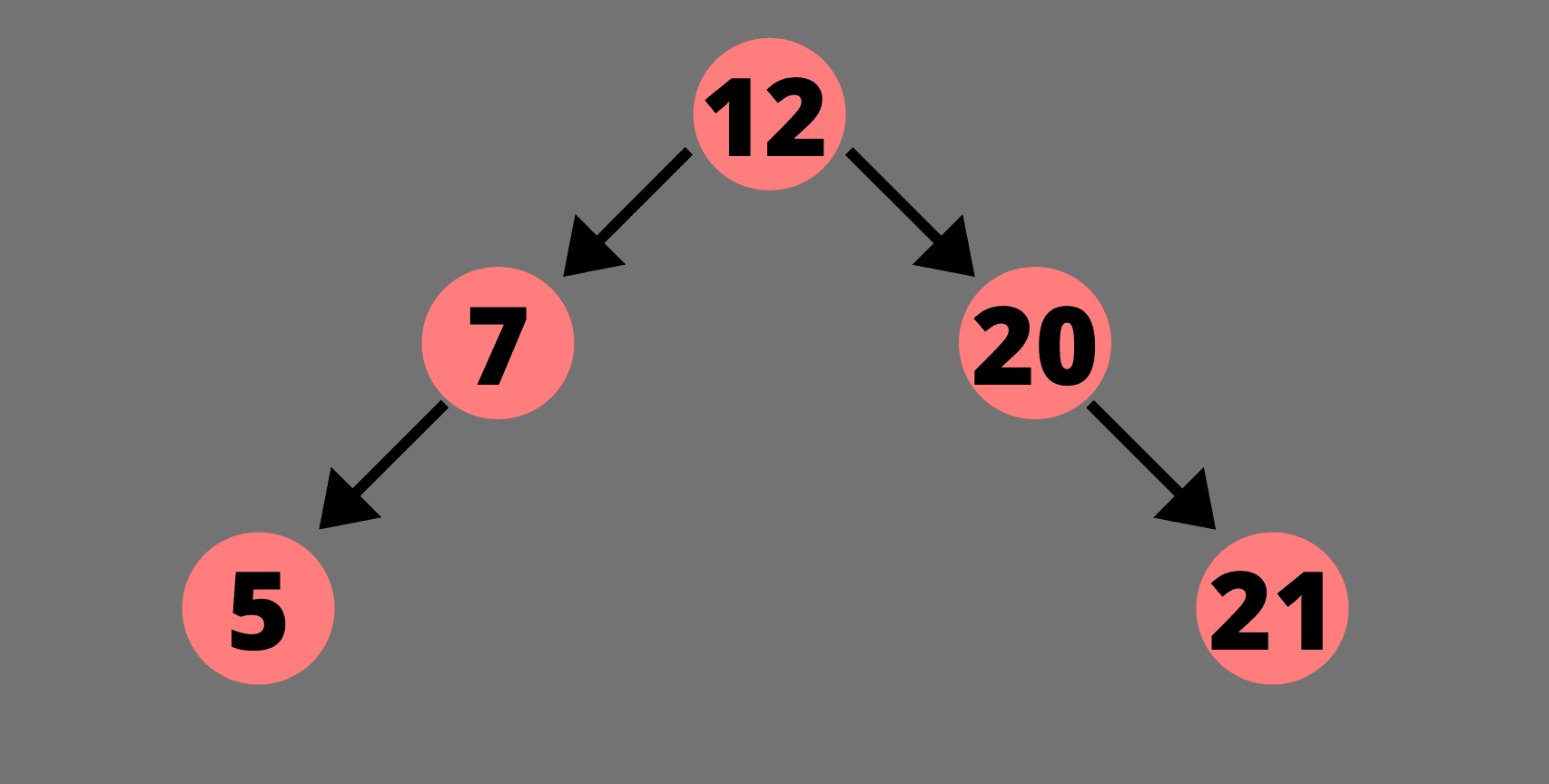
穿越二叉查找树

我们可以用两种不同的方式穿越二叉查找树。让我们学习这两个技巧。

深度优先搜索

顾名思义，在深度优先搜索中，我们将在继续下一个节点之前，尽可能地探索一个特定的节点。它有三种变体，取决于我们探索根、左子和右子的顺序。

Preorder: 如果我们首先访问根节点，然后访问左子节点，最后访问右子节点，那么这种遍历方法称为 Preorder 遍历。

public static void preorder(BSTNode current)
{
    if(current == null)
        return;
    else
    {
        System.out.print(current.value + " ");
        preorder(current.leftChild);
        preorder(current.rightChild);
    }
}

后序:如果我们先探索左边的子节点，然后是右边的子节点，最后访问根节点，那么这种遍历的方法就叫做后序遍历。

public static void postorder(BSTNode current)
{
    if(current == null)
        return;
    else
    {
        postorder(current.leftChild);
        postorder(current.rightChild);
        System.out.print(current.value + " ");
    }
}

inoder:如果我们首先探索左边的子节点，然后访问根节点，最后访问右边的子节点，那么这种遍历的方法称为 inoder 遍历。对于二分搜索法树，有序遍历将按排序顺序返回值。出现这种情况是因为左边的子对象比根对象小，而根对象本身比右边的子对象小。

public static void inorder(BSTNode current)
{
    if(current == null)
        return;
    else
    {
        inorder(current.leftChild);
        System.out.print(current.value + " ");
        inorder(current.rightChild);
    }
}

广度优先搜索

广度优先搜索逐层遍历树。它将首先打印一个级别中的所有值，然后再进入下一个级别。也称为级顺序遍历。下图显示了二叉树的不同层次。以下树的级别顺序遍历将是- 12 7 20 5 9 21。

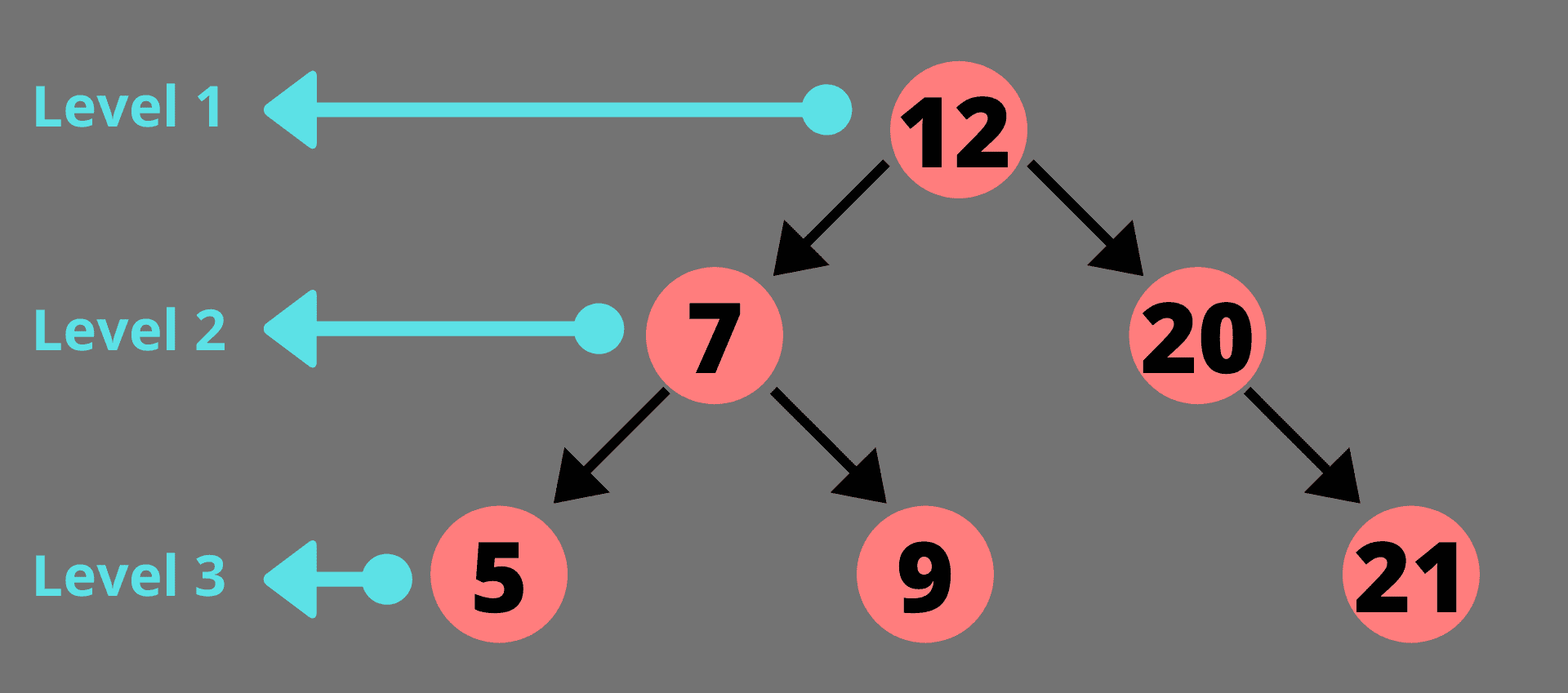
迭代广度优先搜索实现如下所示。队列用于存储节点。

public void static levelOrder(BSTNode current)
{
    if(current == null)
        return;
    Queue<BSTNode> q = new LinkedList<BSTNode>();
    q.add(current);
    while(q.isEmpty() == false)
    {
        BSTNode temp = q.remove();
        System.out.print(temp.value + " ");

        if(temp.leftChild != null)
            q.add(temp.leftChild);
        if(temp.rightChild != null)
            q.add(temp.rightChild);
    }        
}

实践演示

让我们看一下所有上述方法的实际演示。

首先，让我们创建上图所示的二叉树。

public static void main(String args[])
{
    //constructing the tree
    BSTNode root = new BSTNode(12);
    root = insert(7, root);
    root = insert(20, root);
    root = insert(5, root);
    root = insert(9, root);
    root = insert(21, root);
}

现在，让我们使用搜索方法来搜索一些现有的和不存在的值。

public static void main(String args[])
{
    //constructing the tree
    BSTNode root = new BSTNode(12);
    root = insert(7, root);
    root = insert(20, root);
    root = insert(5, root);
    root = insert(9, root);
    root = insert(21, root);

    //searching
    System.out.println(search(7, root));
    System.out.println(search(9, root));
    System.out.println(search(17, root));
}

真 真 假

让我们通过使用不同的遍历技术来打印整个树。

public static void main(String args[])
{
    //constructing the tree
    BSTNode root = new BSTNode(12);
    root = insert(7, root);
    root = insert(20, root);
    root = insert(5, root);
    root = insert(9, root);
    root = insert(21, root);

    //Traversals
    System.out.print("\nPreorder Traversal: ");
    preorder(root);
    System.out.print("\nPostorder Traversal: ");
    postorder(root);
    System.out.print("\nInorder Traversal: ");
    inorder(root);
    System.out.print("\nLevel Order Traversal: ");
    levelOrder(root);
}

前序遍历:12 7 5 9 20 21 后序遍历:5 9 7 21 20 12 中序遍历:5 7 9 12 20 21 级序遍历:12 7 20 5 9 21

让我们删除一些节点并打印遍历。

public static void main(String args[])
{
    //constructing the tree
    BSTNode root = new BSTNode(12);
    root = insert(7, root);
    root = insert(20, root);
    root = insert(5, root);
    root = insert(9, root);
    root = insert(21, root);

    //Deleting nodes
    root = delete(12, root);
    root = delete(9, root);

    //Traversals            
    System.out.println("\n\nAfter deletion");
    System.out.print("\nPreorder Traversal: ");
    preorder(root);
    System.out.print("\nPostorder Traversal: ");
    postorder(root);
    System.out.print("\nInorder Traversal: ");
    inorder(root);
    System.out.print("\nLevel Order Traversal: ");
    levelOrder(root);
}

删除后

前序遍历:20 7 5 21 后序遍历:5 7 21 20 中序遍历:5 7 20 21 级序遍历:20 7 21 5

常见问题

问:二叉树和二叉查找树有什么区别？

对于特定节点，二叉树和二叉查找树树最多可以有两个子节点。在二叉查找树中，左边的子节点应该小于根节点，右边的子节点应该大于根节点，并且这个条件应该适用于所有节点。二叉树在左右子树上没有任何这样的条件。

问:二叉查找树使用二分搜索法算法搜索树中的元素吗？

二叉查找树搜索算法的原理与二分搜索法算法相同。在每次迭代中，我们都将搜索范围缩小到树的一半。这导致 O(log(n))的平均时间复杂度。

问:二叉查找树有哪些真实的用例？

二分搜索法树在三维游戏引擎中非常常用来渲染和生成对象。编译器还使用二分搜索法树来高效解析语法表达式。

摘要

二叉查找树树是普通二叉树的变种。在本教程中，我们学习了如何在二叉查找树中执行插入和删除元素。我们还学习了如何搜索一个元素，以及如何使用广度优先和深度优先的方法遍历整个树。希望你觉得这个教程有帮助，学到了一些新东西。