冒泡排序算法

原文：https://www.studytonight.com/data-structures/bubble-sort

冒泡排序是一种简单的算法，用于对一组给定的n元素进行排序，这些元素以数组的形式提供，具有n个元素。冒泡排序逐个比较所有元素，并根据它们的值对它们进行排序。

如果给定的数组必须按升序排序，那么冒泡排序将从比较数组的第一个元素和第二个元素开始，如果第一个元素大于第二个元素，它将交换两个元素，然后继续比较第二个和第三个元素，以此类推。

如果我们有总共n个元素，那么我们需要重复这个过程n-1次。

它被称为气泡排序，因为随着每一次完整的迭代，给定数组中最大的元素，向最后一个地方或最高的索引冒泡，就像一个水气泡上升到水面一样。

排序是通过逐个遍历所有元素，并将其与相邻元素进行比较，然后在需要时交换它们来进行的。

注意:如果不熟悉数据结构中的排序，首先要学习什么是排序了解排序的基础知识。

实现冒泡排序算法

以下是冒泡排序中涉及的步骤(用于按升序对给定数组进行排序):

从第一个元素开始(index = 0)，将当前元素与数组的下一个元素进行比较。
如果当前元素大于数组的下一个元素，则交换它们。
如果当前元素小于下一个元素，则移动到下一个元素。重复步骤 1 。

让我们考虑一个有值的数组{5, 1, 6, 2, 4, 3}

下面，我们有一个泡泡排序如何排序给定数组的图示。

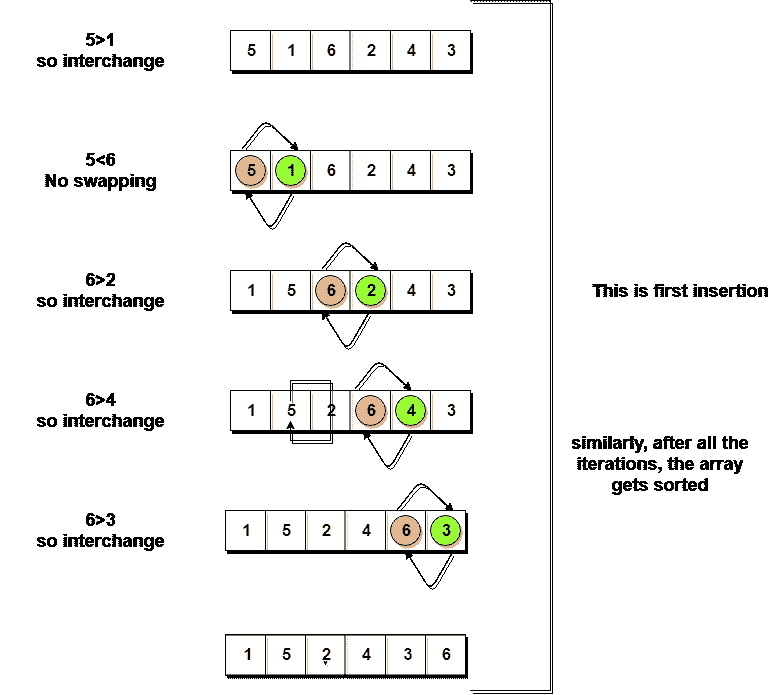
Bubble sort algorithm

因此，正如我们在上面的表示中所看到的，在第一次迭代之后，6被放置在最后一个索引处，这是它的正确位置。

同样，第二次迭代后，5将位于第二个最后一个索引处，以此类推。

是时候为冒泡排序编写代码了:

// below we have a simple C program for bubble sort
#include <stdio.h>

void bubbleSort(int arr[], int n)
{
    int i, j, temp;
    for(i = 0; i < n; i++)
    {
        for(j = 0; j < n-i-1; j++)
        {
            if( arr[j] > arr[j+1])
            {
                // swap the elements
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            } 
        }
    }

    // print the sorted array
    printf("Sorted Array: ");
    for(i = 0; i < n; i++)
    {
        printf("%d  ", arr[i]);
    }
}

int main()
{
    int arr[100], i, n, step, temp;
    // ask user for number of elements to be sorted
    printf("Enter the number of elements to be sorted: ");
    scanf("%d", &n);
    // input elements if the array
    for(i = 0; i < n; i++)
    {
        printf("Enter element no. %d: ", i+1);
        scanf("%d", &arr[i]);
    }
    // call the function bubbleSort
    bubbleSort(arr, n);

    return 0;
}

虽然上面的逻辑将对未排序的数组进行排序，但是上面的算法仍然是无效的，因为根据上面的逻辑，即使数组在第二次迭代之后被排序，外部for循环也将继续执行 6 迭代。

所以，我们显然可以优化我们的算法。

优化冒泡排序算法

为了优化冒泡排序算法，我们可以引入一个flag来监控元素是否在内部for循环中被交换。

因此，在内部for循环中，我们每次都检查元素交换是否正在进行。

如果对于特定的迭代，没有发生交换，这意味着数组已经被排序，我们可以跳出for循环，而不是执行所有的迭代。

让我们考虑一个有值的数组{11, 17, 18, 26, 23}

下面，我们有一个优化气泡排序如何排序给定数组的图示。

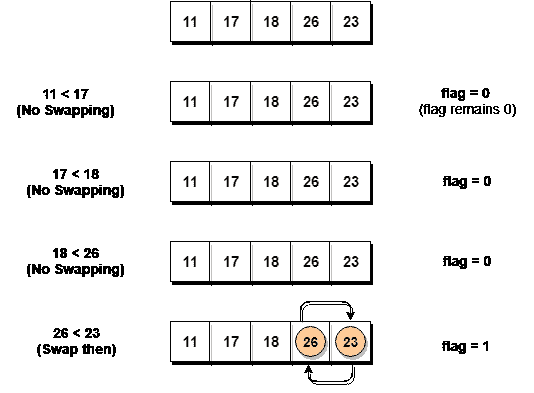
Optimized Bubble sort algorithm

如我们所见，在第一次迭代中，交换发生了，因此我们将flag值更新为1，结果，执行再次进入for循环。但是在第二次迭代中，不会发生交换，因此flag的值将保持0，并且执行将脱离循环。

// below we have a simple C program for bubble sort
#include <stdio.h>

void bubbleSort(int arr[], int n)
{
    int i, j, temp, flag=0;
    for(i = 0; i < n; i++)
    {
        for(j = 0; j < n-i-1; j++)
        {
            // introducing a flag to monitor swapping
            if( arr[j] > arr[j+1])
            {
                // swap the elements
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
                // if swapping happens update flag to 1
                flag = 1;
            } 
        }
        // if value of flag is zero after all the iterations of inner loop
        // then break out
        if(flag==0)
        {
            break;
        }
    }

    // print the sorted array
    printf("Sorted Array: ");
    for(i = 0; i < n; i++)
    {
        printf("%d  ", arr[i]);
    }
}

int main()
{
    int arr[100], i, n, step, temp;
    // ask user for number of elements to be sorted
    printf("Enter the number of elements to be sorted: ");
    scanf("%d", &n);
    // input elements if the array
    for(i = 0; i < n; i++)
    {
        printf("Enter element no. %d: ", i+1);
        scanf("%d", &arr[i]);
    }
    // call the function bubbleSort
    bubbleSort(arr, n);

    return 0;
}

bubble-sort

在上面的代码中，在函数bubbleSort中，如果对于j迭代的单个完整周期(内部for循环)，没有发生交换，那么flag将保留0，然后我们将脱离for循环，因为数组已经被排序了。

冒泡排序的复杂度分析

在冒泡排序中，n-1比较将在第一遍中进行，n-2在第二遍中进行，n-3在第三遍中进行，以此类推。所以比较的总数是，

(n-1) + (n-2) + (n-3) +.....+ 3 + 2 + 1 总和= n(n-1)/2 即 O(n ² )

因此泡泡排序的时间复杂度为 O(n ² ) 。

冒泡排序的主要优点是算法简单。

气泡排序的空间复杂度是0(1)，因为只需要一个额外的内存空间，即temp变量。

此外，最佳案例时间复杂度将是 O(n) ，此时列表已经排序。

以下是气泡排序算法的时间和空间复杂度。

最坏情况时间复杂度【大 O】:O(n²)
最佳案例时间复杂度[大ω]:O(n)
平均时间复杂度【大θ】:O(n²)
空间复杂度: O(1)

既然我们已经学习了气泡排序算法，您也可以查看这些排序算法及其应用: