快速排序算法

原文：https://www.studytonight.com/data-structures/quick-sort

快速排序是不同的排序技术之一，它基于分治的概念，就像归并排序一样。但是在快速排序中，所有繁重的工作(主要工作)都是在将数组划分为子数组时完成的，而在归并排序的情况下，所有真正的工作都发生在合并子数组的过程中。在快速排序的情况下，合并步骤完全不起作用。

也叫分区交换排序。该算法将列表分为三个主要部分:

  1. 小于枢轴元素的元素
  2. 枢轴元素(中心元素)
  3. 大于枢轴元素的元素

Pivot 元素可以是数组中的任意元素，可以是第一个元素，最后一个元素，也可以是任意随机元素。在本教程中，我们将最右边的元素或最后一个元素作为轴。

例如:在阵{52, 37, 63, 14, 17, 8, 6, 25}中，我们以25为枢。所以第一遍过后，名单会这样改。

{ 6 8 17 14 25 63 37 52 }

因此，在第一次通过后，枢轴将被设置在其位置，所有元素在其左侧较小，所有元素在其右侧较大。现在6 8 17 14和63 37 52被认为是两个独立的 sunarrays，相同的递归逻辑将被应用于它们，我们将继续这样做，直到整个数组被排序。

快速排序的工作原理是什么？

以下是快速排序算法中涉及的步骤:

  1. 在选择一个元素作为轴之后，这是我们这里数组的最后一个索引，我们第一次划分数组。
  2. 在快速排序中，我们称之为分区。将数组分解为 2 个子数组并不简单，但在划分的情况下，数组元素的位置应使所有小于枢轴的元素位于枢轴的左侧，所有大于枢轴的元素位于枢轴的右侧。
  3. 并且枢轴元件将处于其最终的分类位置。
  4. 左侧和右侧的元素可能没有排序。
  5. 然后我们选取子数组、轴左侧的元素、轴右侧的元素，通过选择子数组中的轴对它们进行分区。

让我们考虑一个有值的数组{9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

下面，我们有一个图片表示排序将如何快速排序给定的数组。

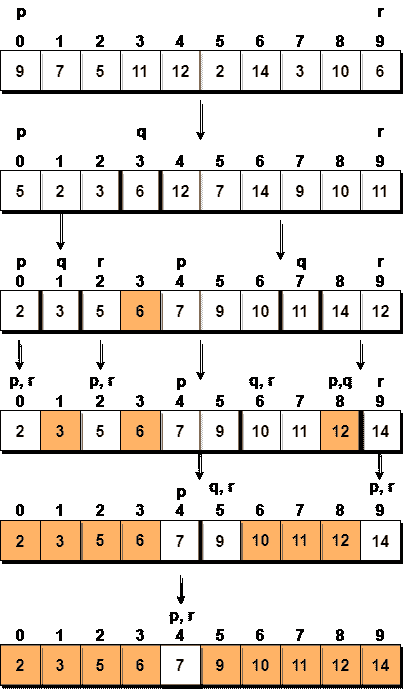
How Quick Sort algorithm works

在第一步中，我们选择最后一个元素作为枢轴，在这种情况下是6，并调用partitioning，因此重新排列数组，使得6将被放置在其最终位置，并且在其左侧将有所有小于它的元素，在其右侧，我们将有所有大于它的元素。

然后我们选择左边的子数组和右边的子数组，为它们选择一个枢轴，在上图中，我们选择3作为左边子数组的枢轴，选择11作为右边子数组的枢轴。

我们再次呼吁partitioning。

实现快速排序算法

下面我们有一个实现快速排序算法的简单 C 程序:

// simple C program for Quick Sort
#include <stdio.h>
int partition(int a[], int beg, int end);  
void quickSort(int a[], int beg, int end);  
void main()  
{  
    int i;  
    int arr[10]={90,23,101,45,65,28,67,89,34,29};  
    quickSort(arr, 0, 9);  
    printf("\n The sorted array is: \n");  
    for(i=0;i<10;i++)  
    printf(" %d\t", arr[i]);  
}  
int partition(int a[], int beg, int end)  
{  
    int left, right, temp, loc, flag;     
    loc = left = beg;  
    right = end;  
    flag = 0;  
    while(flag != 1)  
    {  
        while((a[loc] <= a[right]) && (loc!=right))  
        right--;  
        if(loc==right)  
        flag =1;  
        else if(a[loc]>a[right])  
        {  
            temp = a[loc];  
            a[loc] = a[right];  
            a[right] = temp;  
            loc = right;  
        }  
        if(flag!=1)  
        {  
            while((a[loc] >= a[left]) && (loc!=left))  
            left++;  
            if(loc==left)  
            flag =1;  
            else if(a[loc] < a[left])  
            {  
                temp = a[loc];  
                a[loc] = a[left];  
                a[left] = temp;  
                loc = left;  
            }  
        }  
    }  
    return loc;  
}  
void quickSort(int a[], int beg, int end)  
{  
    int loc;  
    if(beg<end)  
    {  
        loc = partition(a, beg, end);  
        quickSort(a, beg, loc-1);  
        quickSort(a, loc+1, end);  
    }  
}

output-quick-sort

快速排序的复杂度分析

对于其中划分导致子数组不平衡的数组，在左侧没有元素，所有元素大于枢轴，因此在右侧。

而如果继续得到不平衡的子阵，那么运行时间就是最坏的情况，也就是O(n<sup>2</sup>)

如果划分导致几乎相等的子阵，那么运行时间最好，时间复杂度为 O(n*log n) 。

最坏情况时间复杂度【大 O】:O(n2)

最佳案例时间复杂度[大ω]:O(n * log n)

平均时间复杂度[大-θ]:O(n * log n)

空间复杂度: O(n*log n)

我们现在知道，如果分区后产生的子阵分区不平衡，快速排序需要更多的时间才能完成。如果有人知道你一直选择最后一个索引作为枢纽，他们可以故意给你提供数组，这将导致最坏情况下的快速排序运行时间。

为了避免这种情况，您也可以随机选择轴元素。这在算法上不会有什么区别，因为你所需要做的就是从数组中选择一个随机元素，用最后一个索引处的元素交换它，使它成为枢轴，然后继续快速排序。

  • 快速排序需要的空间很少，只需要O(n*log n)额外空间。
  • 快速排序不是一种稳定的排序技术，因此它可能会在排序时改变列表中两个相似元素的出现。

现在我们已经学习了快速排序算法，您也可以查看这些排序算法及其应用: