使用队列实现栈

原文：https://www.studytonight.com/data-structures/stack-using-queue

栈是后进先出(LIFO) 结构，即栈中最后添加的元素先取出。我们的目标是实现一个使用队列的栈，该栈将使用两个队列，并以这样的方式设计它们:弹出操作与出列相同，但是推送操作将有点复杂并且更昂贵。

使用队列实现栈

假设我们已经为 Queue 实现了一个类，我们首先为 Stack 设计这个类。它将有方法push()和pop()以及两个队列。

class Stack
{
    public:
    // two queue
    Queue Q1, Q2;
    // push method to add data element
    void push(int);
    // pop method to remove data element
    void pop();
};

在栈中插入数据

由于我们使用的队列是先进先出(FIFO) 结构，即先添加的元素先取出，所以我们将执行推送操作，这样每当有弹出操作时，栈总是弹出最后添加的元素。

为此，我们需要两个队列，Q1和Q2。每当调用推操作时，我们将把Q1的所有元素入队(在这种情况下是移动)到Q2，然后把新元素入队到Q1。在此之后，我们将所有元素从Q2排队(在这种情况下移动)回到Q1。

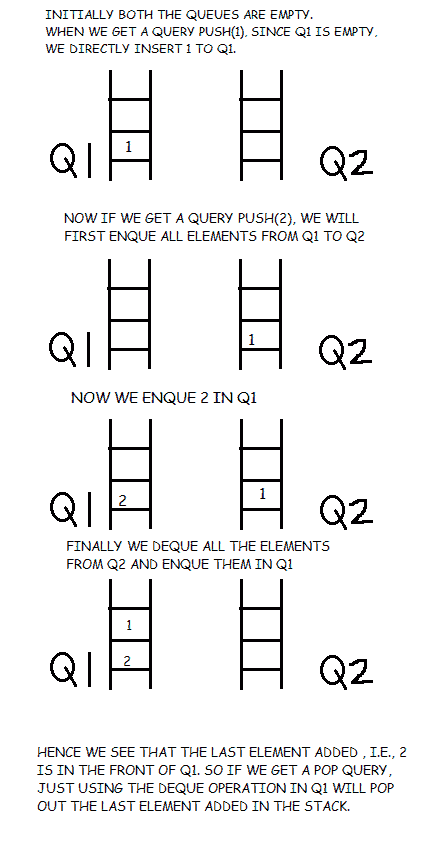
让我们在代码中实现它，

void Stack :: push(int x)
{
    // move all elements in Q1 to Q2
    while(!Q1.isEmpty())
    {
        int temp = Q1.deque();
        Q2.enque(temp);
    }

    // add the element which is pushed into Stack
    Q1.enque(x);

    // move back all elements back to Q1 from Q2
    while(!Q2.isEmpty())
    {
        int temp = Q2.deque();
        Q1.enque(temp);
    }
}

你现在一定很清楚，为什么我们使用两个队列。实际上队列Q2只是为了在执行操作时暂时保存数据。

这样我们就可以保证每当调用 pop 操作时，栈总是会弹出Q1队列中添加的最后一个元素。

从栈中删除数据

就像我们上面讨论的，我们只需要对我们的队列Q1使用出列操作。这将为我们提供栈中添加的最后一个元素。

int Stack :: pop()
{
    return Q1.deque();
}

时间复杂度分析

当我们使用队列实现栈时，推操作变得昂贵。

• 推送操作:0(n)
• 弹出操作:0(1)

结论

当我们说“使用队列实现栈”时，我们指的是如何让队列表现得像一个栈，毕竟它们都是逻辑实体。所以任何数据结构作为一个 Stack，都应该有push()方法在顶部添加数据，有pop()方法从顶部移除数据。这正是我们所做的，并因此实现了让一个队列(在本例中是两个队列)表现为一个栈。